Parallelization of Multi-Objective Evolutionary Algorithms

In the context of Multi-Objective Evolutionary Algorithms (MOEAs), parallelization becomes a natural and effective strategy when multiple computing cores or distributed computing nodes are available. This is due to the intrinsic characteristics of evolutionary algorithms, which make them well-suited for concurrent execution. In fact, such problems are often referred to as embarrassingly parallel, meaning that their parallelization is not only feasible but also remarkably straightforward.

This trait is particularly evident in evolutionary algorithms, where different individuals or subpopulations can be evaluated or evolved independently for large parts of the process.

General Parallelization Strategies for Evolutionary Algorithms

There are three main parallelization models that can be applied to both single-objective and multi-objective evolutionary algorithms:

1. Coordinator-Workers Model

In this approach, a central coordinator is responsible for generating the offspring population and delegating the computation of the objective functions to multiple workers. Each worker evaluates its assigned individuals and returns the results to the coordinator. Then, the coordinator aggregates these evaluations and performs the selection step to generate the next generation.

This model introduces a synchronization barrier since the coordinator must wait for all evaluations to be completed before proceeding.

In the island model, each CPU (or computing node) runs a separate sub-population that evolves independently. After a fixed number of generations, a migration step is executed, allowing some of the best individuals to move from one island to another.

This method encourages diversity and helps spread good solutions across the islands, fostering better exploration of the search space while keeping the islands informed of global progress.

In the cellular model, individuals are placed on a structured grid, and evolution is spatially constrained. An individual can interact and exchange genetic material only with its neighboring nodes, based on a predefined neighborhood structure. This localized interaction leads to slower but more diversified convergence.

Multi-Objective Specific Parallel Strategies

While the previous models are general-purpose, some strategies have been specifically designed to exploit the objective space in multi-objective optimization. Among these:

• Cone Separation Method (cspMEA): Branke, Schmeck, Deb, and Reddy (2004)
• Microcones Separation Method (mspMEA): Cococcioni (2016)
• Additional recent variants are continually being proposed, as outlined in the survey by Harada and Alba (2020).

cspMEA – Cone Separation Multi-Objective Evolutionary Algorithm

The cone separation method (cspMEA) is a strategy designed to parallelize multi-objective evolutionary algorithms by leveraging the decomposition of the objective space. Specifically, the global Pareto front is partitioned into multiple cones, each assigned to a different worker (processor). This partitioning allows the workers to focus on different regions of the front, avoiding redundancy and promoting coverage. Compared to a random assignment of individuals to workers, cspMEA offers a more structured and informed parallelization approach.

This pseudocode outlines the standard procedure of cone-separated NSGA-II, where each generation includes a step for verifying whether individuals still belong to their assigned cone. If not, they are migrated accordingly. The algorithm ensures constraint enforcement and encourages specialization of each worker on its own cone.

Advantages

• Informed decomposition of objective space: It assigns individuals to regions of the Pareto front, ensuring a more structured parallel search than random assignment.
• Natural mapping to parallel architectures: Each processor handles a distinct portion of the objective space, allowing distributed, semi-independent optimization.

Limitations and Illustrative Issues

1. Local Pareto fronts may not align with the global Pareto front We observe that cone 4’s local Pareto front is completely dominated by solutions found in cone 3. This means that the best solutions identified by processor 4 are not part of the true global Pareto front. Only cones 1, 2, 3, and 5 contribute valid Pareto-optimal solutions globally. This limitation demonstrates how regional optimization may lead to misleading convergence within a cone, even when those solutions are globally suboptimal.

   

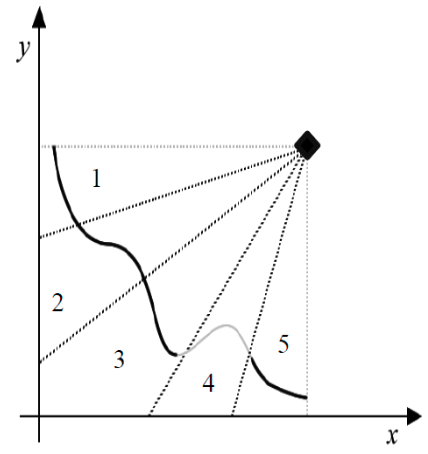
2. Uneven distribution of solutions across cones Fig. 5 illustrates this issue with two subfigures:

   • In (a), we see three local Pareto fronts from three cones. Cone 2 has a discontinuous front, resulting in a higher density of solutions compared to cones 1 and 3, which may create imbalance.
   • In (b), the same problem is solved with a single processor running NSGA-II across the entire front, ensuring a uniform distribution of solutions. This highlights that dividing the front into cones can prevent a balanced spread of individuals, especially when local regions are not equally “rich” in Pareto-optimal points.

   

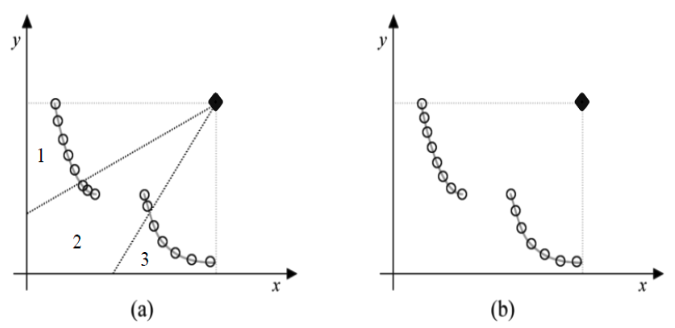
3. Sensitivity to the shape of the Pareto front

   The following figure offers deeper insight:

   • Subfigure (a) shows a situation where cone 2 again ends up with higher density due to the shape of the front, far from the unit circle.
   • In contrast, (b) presents the same front handled by NSGA-II globally: the crowding distance is calculated on the entire front, leading to better distribution.
   • Subfigure (c) shows a well-behaved front, close to a unit circle centered at the nadir point. In this special case, cspMEA does result in a uniform distribution, as the geometry aligns with the cone divisions. These observations emphasize that cspMEA performs best when the global front aligns well with the cone structure. However, in real-world problems with irregular Pareto fronts, the strategy may fail to ensure global coverage and uniformity.

   

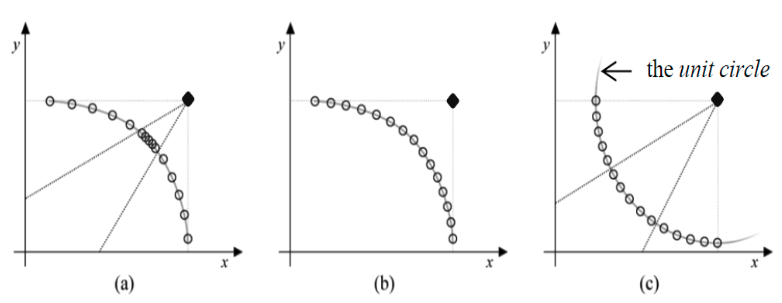
4. Unbounded migration and communication cost In cspMEA, whenever a solution violates the constraints of its assigned cone, it must be migrated. There is no soft mechanism to delay or limit this process, meaning the migration rate can be high and unpredictable. Migration involves data transfer between processors or machines, which can significantly degrade performance in distributed systems, negating the advantages of parallel execution.

mspMEA – Microcones Separation Parallel MOEA

To overcome the structural limitations of cone-based parallelization seen in cspMEA, the Microcones Separation Parallel Multi-Objective Evolutionary Algorithm (mspMEA) was introduced. The fundamental innovation lies in subdividing the objective space into smaller, more numerous regions called microcones, which offer finer granularity and improved flexibility in the parallel distribution of the search process.

Conceptual Design

Instead of assigning an entire cone to a single processor, mspMEA divides each cone into several microcones. These microcones are then interleaved across processors, such that each processor is responsible for non-contiguous but systematically assigned regions of the objective space. For example, in a setup with three cones and three microcones per cone, processor 1 will manage microcones labeled “1” from each cone, processor 2 handles all the “2”-labeled microcones, and so on. This architecture allows each processor to contribute to the exploration of multiple portions of the Pareto front, leading to greater diversity and robustness in the population.

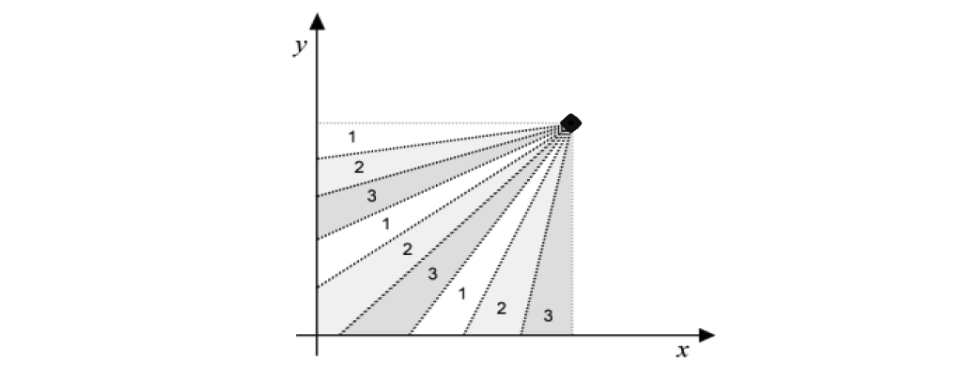
One of the main enhancements over cspMEA is the local knowledge a processor gains from managing multiple and distributed regions of the front. A processor can detect whether the solutions it maintains in one microcone are dominated by those in another of its assigned microcones. This capability allows the processor to discard non-Pareto-optimal regions early, even without explicit inter-processor communication. While this doesn’t eliminate all possible suboptimal contributions to the global front, it mitigates the risk of misrepresenting the global Pareto front significantly more than the original cone-based approach.

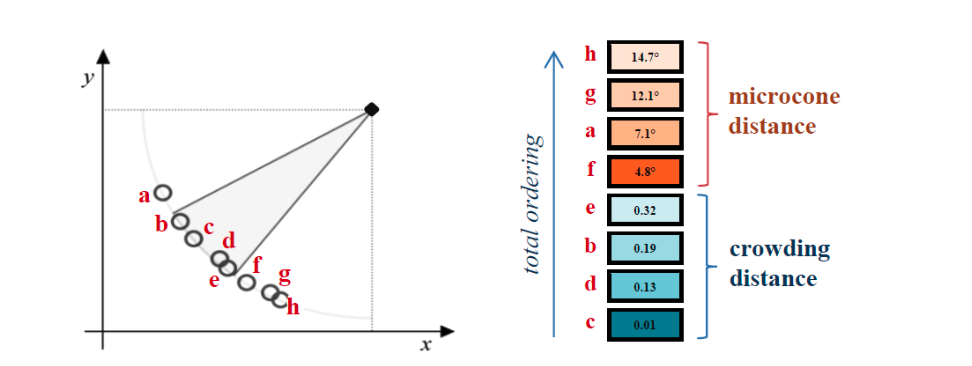
Selection Process and the Role of Microcone Distance

To form the next generation, mspMEA introduces a refined selection strategy. Within each microcone, solutions are ranked based on crowding distance, as in NSGA-II, promoting diversity among close competitors.

However, when the number of viable solutions within a microcone is insufficient, the algorithm allows selecting individuals outside the microcone—but gives priority to those closer to its direction. For this purpose, a new metric is introduced: the microcone distance, which measures the angular deviation between a candidate solution and the central axis of the microcone.

This dual-criteria system enables a flexible yet focused selection:

• Inside the microcone: use crowding distance to preserve spread and diversity.
• Outside the microcone: use microcone distance to select the closest eligible solutions.

The combined ordering ensures that solutions from within the microcone are preferred, but in their absence, the selection gracefully degrades to nearby options without introducing hard discontinuities.

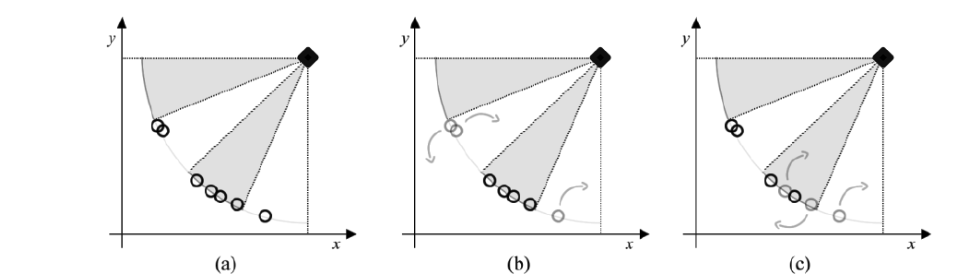
Unlike cspMEA, which enforces hard constraints on cone membership and mandates deterministic migration, mspMEA introduces a soft-constraint approach. Rather than requiring immediate migration of all out-of-place solutions, the algorithm considers their proximity and selective value.

This leads to a more adaptive and scalable migration policy:

• Solutions that are only marginally outside their designated region may still be retained if they contribute effectively.
• Migration occurs probabilistically or selectively, minimizing unnecessary communication costs in parallel settings.

The ranking process in mspMEA maintains the use of non-dominated sorting to identify Pareto-optimal candidates, just like NSGA-II and cspMEA. However, while NSGA-II employs crowding distance to handle selection and diversity, and cspMEA relies on strict region constraints, mspMEA replaces the second step with the microcone assignment strategy. This shift offers a more spatially-aware, flexible method for distributing solutions across the population.

MspMEA provides a robust and practical solution to several key issues of parallel evolutionary multi-objective optimization:

• It improves load balancing across processors by ensuring each one contributes to diverse regions.
• It reduces the risk of redundant or dominated solutions through intra-processor awareness.
• It preserves diversity and promotes convergence via a nuanced combination of crowding and angular proximity.
• It softens migration policies, which reduces overhead and increases performance in parallel systems.

References